Problème SD, Opérateur Trace, Schémas d'Identification et Codes de Goppa

Présentée le 7 Juillet 1995 devant le jury composé de:

Rapporteurs	Pascale Charpin	Directeur de recherche à l'INRIA Rocquencourt
	Jacques Stern	Professeur à l'Ecole Normale Supérieure de Paris
Président	Pierre Liardet	Professeur à l'Université d'Aix-Marseille I
Directeur	Sami Harari	Professeur à l'Université de Toulon et du Var
Membres	Guy Robin	Professeur à l'Université de Limoges
	Jacques Wolfmann	Professeur à l'Université de Toulon et du Var

Dans cette thèse, je m'intéresse essentiellement au problème suivant:


''Comment prouver son identité à un interlocuteur en ayant une puissance de calcul et uneplace mémoire limitée, et en minimisant les échanges d'informations entre les deuxintervenants (nombre de bits transmis lors du processus d'identification ou débit detransaction) ?''


Ceci dans le but d'une application pratique de type cartes à puces.





Les deuxparties qui communiquent sont respectivement appelées le ''prouveur'' et le ''vérifieur''. Pourrésoudre un tel problème je me suis intéressé à la théorie complexe des systèmes interactifsde preuve à divulgation nulle introduite en 1985 par Goldwasser, Micali et Rackoff.Dans ces systèmes le prouveur détient un secret s, solution d'un problème P public réputé être''difficile'' à résoudre (i.e non résoluble en temps polynomial). Ceci le caractérise. Pours'identifier, il démontre au vérifieur qu'il connaît effectivement la solution s du problème P.Dans les systèmes interactifs de preuve à divulgation nulle, une telle preuve s'effectue à l'aided'une succession d'échanges de questions/réponses entre le prouveur et le vérifieur. A la fin duprocessus le vérifieur est convaincu avec une probabilité arbitrairement proche de 1 del'identité du prouveur. De plus les échanges effectués avec le prouveur ne contiennentstrictement aucune information sur le secret s (sinon qu'il est en la possession de cedernier), si bien qu'il est impossible à un vérifieur malhonnête d'usurper l'identité du prouveur.

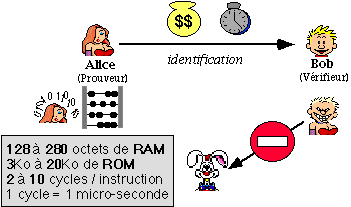
Si vous voulez en savoir plus, cliquez ici.